Debunking an Illusion...
Take a good look at this illusion:
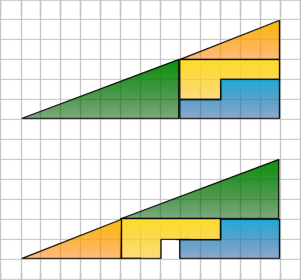
Figure 1. The Illusion
Where did the 1x1 whole come from?
I came across this illusion here and a similar one here. I couldn't believe it. Is math really flawed? No way, it couldn't, right? I eventually figured it out (with a little help, I admit). Once you know the trick it's actually quite obvious.
The grid lines add to the illusion that the large triangle has a straight hypoteneuse but it actually turns out that it doesn't. At first glance you are led to believe that it has a slope of 13:5 but in fact that green and orange triangles have a different slope, 8:3 and 5:2 respectively.
This means that the hypotenuse of the large triangle actually has a bump in it. In the top version the bump is concave and in the bottom version it is convex. This is a little easier to notice without the grid distracting you:
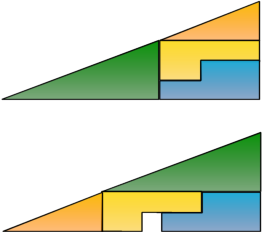
Figure 2. The Illusion Without The Gridlines
Notice the bend in the hypoteneuse of the big triangle.
If you were to use a paint program or draw this out on ruled paper you could clearly see that the top hypotenuse bumps in and the bottom one bumps out. Since the area of shapes cannot increase simply by changing their position, the convex hypotenuse in the bottom illusion creates enough room for a whole of dimension 1x1. It just so happens that it's a square because of the shapes chosen to add to the illusion.
Don't believe me? Take a 1x1 square out of the top triangle and then place it on the hypotenuse of the top triangle. Now stretch two opposing ends to each end of the hypotenuse. Can you imagine how the square becomes thinner as you strech it? In fact, the square becomes so thin that you barely notice it and in fact wind up with the bottom triangle, hence the illusion.
Still don't believe me? Okay, let's do some math.
First we'll start of by calculating the hypoteneuse values for the small triangles and the large triangle as how the illusion would have you believe it is so that you are convinced that they are not all the same. For this we use the Pythagorean Theorem (recall a² + b² = c²).
- Hypotenuse of illusion triangle: c = sqrt(13² + 5²) = 13.92838828
- Hypotenuse of green triangle: c = sqrt(8² + 3²) = 8.544003745
- Hypotenuse of orange triangle: c = sqrt(5² + 2²) = 5.385164807
Figure 3 below shows these values with the large triangle as how the illusion would have you believe it. Since 8.544003745 + 5.385164807 = 13.92916855 and that that is larger than 13.92838828 we know that the hypotenuse of the large triangle cannot be straight.
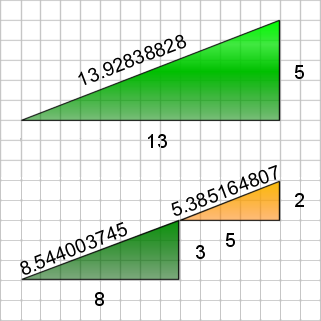
Figure 3. The Hypotenuse Values
So now on to show that the bend in the hypotenuse actually contains the space of a 1x1 object. To do that we must calculate the area of the bend. Figure 4 below shows an exaggeration (i.e. not to scale) of the bend so that you can follow what we are trying to do.
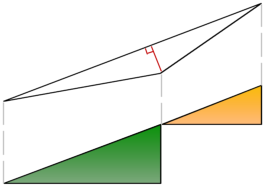
Figure 4. The Hypotenuse Area (Not To Scale)
Figure 5 below is exaggerated even further, this time with the angles we will need. The intent of Figures 4 and 5 is not to change the ratios, rather merely to make it clearer what we are calculating since the bump is so small.
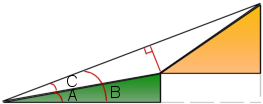
Figure 5. The Angles Needed (Not To Scale)
Now to calculate the angles we'll need to use some geometry. Recall that sin(Θ) = a/c, cos(Θ) = b/c, and tan(Θ) = a/b. We won't evaluate any values to avoid rounding errors (but you can do so if it helps you follow; be sure to do it in radians, not degrees!). So we have:
- A = arctan(3/8)
- B = arctan(5/13)
- C = B-A = arctan(5/13)-arctan(3/8)
Now we can use the angles to find the area of the bump (the white triangle in Figures 4 and 5). The easiest way to that is to split up the area into two right angle triangles. To do that we need to find the height of the triangle (the red bar). We can use angle C, the hypotenuse of the green triangle, and the sin rule:
- Height = hypotenuse * sin(C) = sqrt(8² + 3²) * sin(C) = 0.0717958159
The next move is to split the area's base into two pieces along it's height to form to separate right triangles using the Pythagorean Theorem again:
- Base of lower half = sqrt([sqrt(8² + 3²)]² - Height²) = 8.543702088
- Base of upper half = sqrt(13² + 5²) - Base of lower half = 5.38468619
Now we can find the area of both triangles. Recall that the area of a right triangle is the base times half it's height.
- Area of lower triangle = 0.3067010309
- Area of upper triangle = 0.1932989691
The sum of the two areas? You guessed it, 0.5! If you were to do the same calculations for the convex bump you'd see that it also comes to 0.5. So although the large triangle looks like it has an area of 13*0.5*5 = 32.5, it really only has an area of 32 (you can verify this by calculating the area of all the individual objects).
So no, math is not flawed. Good thing too.
